OPERACIONES CON VECTORES

 OPERACIONES CON VECTORES

Así como se pueden sumar números reales, a los vectores también se les pueden sumar, restar y multiplicar por una escalar(número real cualquiera)

Producto de un vector por un escalar: 

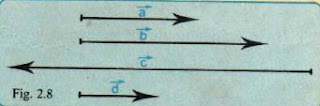
Observa los vectores de la figura de la izquierda.

a. Si representamos el vector unidad con una longitud de 2,5 cm, determina la longitud o magnitud de cada uno de los vectores de la figura.

b. Compara la magnitud del vector a, con la magnitud de los demás  vectores. ¿Cuántas veces es mayor o menor cada uno de los vectores con respecto  al vector a?

c. Expresa cada uno de los vectores en función del vector a.

d. ¿Tienen todos los vectores la misma dirección?¿por qué?

e. ¿Tienen el mismo sentido?

f. Si al vector a, se le asigna el sentido dado en la figura, el vector c que tiene sentido contrario, ¿Cómo se expresaría en función del vector a?

Suma de Vectores:

Para sumar gráficamente dos o más vectores, se colocan  los vectores de tal forma que el origen de uno se conecte con la punta del otro y así sucesivamente, el resultado es el vector que resulta de unir el origen del primer vector con la flecha, cabeza o punto terminal del último vector.

Para sumar vectores de forma analítica se deben tener en cuenta la dirección, sentido y la relación entre cada vector, así:

a. Ángulo entre los dos vectores =0°, es decir, actúan en la misma dirección y el mismo sentido.

b. Ángulo entre los dos vectores =180°, es decir, actúan en la misma dirección y en sentido contrario.

c. Ángulo entre los dos vectores =90°, es decir, tienen distinta dirección y distinto  sentido.

d. Cuando el angulo es diferente de 0°, 90° o de 180°, se aplica la ley del Coseno:

- Suma de vectores por descomposición rectangular. Cuando se tienen más de dos vectores para sumar en un plano  cartesiano, es más convemniente descomponer cada vector en sus componenetes rectangulares y seguir el proceso que se describe.

Con el siguiente ejercicio aprenderás a sumar dos o más vectores, descomponiéndolos rectangularmente. Halla la suma de los vectores a,  b, y c, que aparecen ligados a un sistema de coordenadas cartesianas,  sabiendo que forman ángulos de 35°, 180°, -50 respectivamente y en posición normal respecto a X.

a. Halla los componentes rectangulares de cada vector y consigna dichos resultados en una tabla  como ésta: 

 

ax  =
ay =	a.Sen35º	5cm.Sen35º
bx =
by =
cx =
cy=

b. Efectúa la suma en cada uno de los ejes,  R_x  R_y, teniendo en cuenta el  siguiente convenio:

- Las componentes en las direcciones de los semiejes positivos son positivos.

- Las componentes en las direcciones de los semiejes negativos son negativos.

- Dibuja un eje de coordenadas cartesiano y sobre este representa la resultante de las componentes en x (R_x) y la resultante de las componentes en y (R_y).

c. Aplica el teorema de Pitágoras a las componentes resultantes para hallar la magnitud del vector suma R =    ?   

Para afianzar más tu conocimiento, te infito que analices el siguiente simulkador de operaciones con vectores: OPERACIONES CON VECTORES

Cualquier inquietud escribe en los comentarios.

Tomado de Investiguemos 10°.Ed. Voluntad.